After the multiplication facts are learned, the next step is to multiply larger numbers.
Let’s look at several methods including the Lattice method.

Traditional Method:
Step 1.
Multiply the ones. ( 4 x 2 =8)

3 4
X 2
---------------
...8 (The periods in front of the eight and any other number in this article can be ignored. They are for formatting purposes only)

Step 2.
Multiply 2 by the tens place. Notice the 6 is written in the tens place because you are actually multiplying 30 x 2 = 60 and thus end up with 6 tens.

3 4
x 2
----------------
6 8
We’re done!

Example 2
Multiply 8 x 7 = 56. since the largest number any place value can hold is 9, we must leave the six in the ones place, but carry the 5 to the tens place. Notice the”+” in front of the five to remind us to add it later.

+5
.. 3 8
X 7
----------------
... 6

Step 2
Multiply 7 times the tens place and add the number carried in the last step.
(7 x 3 = 21 + 5 = 26 tens)
Again, the answer is larger than 9, so write the 6 in the tens place. Since, there is no place to carry the 2, place it in front of the 6.

+5
..3 8
X 7
----------------
266
We’re done!


Now, let’s multiply a two-digit number by a two-digit number.

One Way: This method uses the expanded notation.
(Ignore the periods in front of the numbers. They are for formatting purposes only.)
5 6
x 4 3
-------
…18 < --- 6 x 3
..150 < --- 50 x 3
..240 < --- 6 x 40
2000 < --- 50 x 4
--------
2408 < --- (Add 18 +150 + 240 + 2000)


Traditional Method:

Step 1
+1
..5 6
X 4 3
----------
168 < --- 56 x 3

Step 2
+2
.. 5 6
X 4 3
------------
168 < --- 56 x 3
2240 < --- 56 x 40
--------
2408 < ---- (168 + 2240)





Lattice Method
Let’s use the same factors, 56 x 43





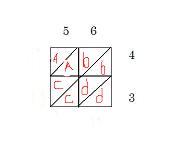
Write factors outside of the box.
Box a – enter answer for 5 x 4 = 20
Box b – enter answer for 6 x 4 = 24
Box c – enter answer for 5 x 3 =15
Box d – enter answer for 6 x 3 = 18

Look below:










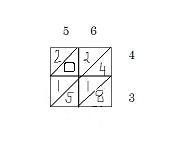
Next, Add numbers in the diagonals.








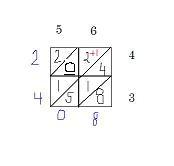
The answer is 2,408
56 x 43 = 2,408


Which method do you prefer?